|
THE VIDEO component of the Third International Mathematics and Science Study (TIMSS) was the first attempt ever made to use videotape to study national probability samples of teachers at work. In this article, we present a brief overview of this unprecedented study, which involved detailed analysis and comparison of eighth-grade mathematics teaching in three countries: Germany, Japan, and the United States. We also discuss implications of the video study for the improvement of classroom mathematics teaching in the United States.
Collecting national samples of teaching can serve two important purposes. First, it gives us solid information about the processes of teaching and learning inside U.S. classrooms, information that is crucial for developing sound education policies. Efforts to improve student learning succeed or fail inside the classroom, a fact that has too often been ignored by would-be reformers. Setting standards for content and performance is an important first step. But student learning will not be improved merely by setting standards and holding teachers accountable. We must study directly the processes that lead to learning in the classroom, for if we do not understand these processes we will have little chance of improving them. Most other professional and industrial fields have determined that improving the quality of the processes is the surest road to improving products, but we in education have yet to learn this lesson. The videotape study of classroom instruction allows us to refocus on teaching processes, with the aim of improving students' learning.
National samples of teaching also enable us to compare U.S. teaching methods with those used in other countries. This comparison allows us to see teaching in a new way. Teaching is a cultural activity.1 It is an everyday event that occurs throughout all parts of American society. Over time, we have developed norms and expectations for teaching that are widely shared and passed along as one generation of students becomes the next generation of teachers.2 Because our models of how teaching should look are so widely shared and so familiar, they become nearly invisible. We come to believe that this is the way teaching must be. When we observe teaching in other countries, these accepted and unquestioned practices are brought to light, and we see that we teach the way we do because we choose to teach this way. This realization is crucial because it opens up new possibilities for how we might improve teaching.
Conducting the TIMSS Video Study
U.S. students performed poorly in the Second International Mathematics Study (SIMS), conducted in the 1980s. Consequently, as planning commenced for the TIMSS, there was great interest in being able to go beyond the cross-national achievement data to focus on the underlying processes that produce achievement. Instructional processes in the classroom were assumed to be an important cause of student learning. But how could something as complex as teaching be studied on a large scale, across cultures?
One approach is to give teachers a questionnaire asking them to describe their instructional practices. Although such a questionnaire had been administered as part of SIMS, there are problems with this approach. Even within the U.S., we lack shared meanings for the words we use to describe teaching. One teacher will call something "problem solving" while her colleague next door calls the same thing a "routine exercise." The problem of no shared language is compounded in a cross-cultural questionnaire study. The responses are nearly impossible to interpret.
Thus the decision was made to collect direct information on teaching by videotaping classroom instruction. Video had long been used for small-scale, in-depth qualitative research but had never been employed on such a large scale before. For this reason, the scope of the study was limited to one of the three grade levels studied in TIMSS (eighth grade) and to three of the 41 TIMSS countries (Germany, Japan, and the United States). Germany and Japan were chosen because they are both viewed as important economic competitors of the U.S. Japan is of special interest because it has repeatedly scored near the top in international comparisons of mathematics achievement.
Three straightforward goals guided the study: 1) to learn how eighth-grade mathematics is taught in the United States, 2) to learn how eighth-grade mathematics is taught in the two comparison countries, and 3) to learn how American teachers view reform and to see whether they are implementing teaching reforms in their classrooms. To achieve these goals, a number of methodological hurdles had to be cleared.
Sampling. If we wanted to use video to paint national portraits of eighth-grade mathematics instruction, we needed to be sure that the videotapes we analyzed were representative of instruction in each country. A number of issues were considered. First, how should classrooms be selected? Fortunately, the TIMSS sampling plan was highly sophisticated. For this reason, it was possible to construct the video sample as a random subsample of the full TIMSS sample.3 Not only were specific teachers selected, but specific class periods as well. No substitutions were allowed, either by another teacher within the same school or by another class period with the same teacher. The final video sample included 231 classrooms: 100 in Germany, 50 in Japan, and 81 in the United States.
Having chosen the classrooms, we next needed to decide how many lessons to videotape in each one. In the end, we videotaped one lesson in each classroom. Although this enabled us to study the largest number of teachers within our budget, it precluded our studying some important parts of the teaching process, such as the methods teachers use for linking lessons together into units.
Finally, we wanted to be sure that our sample was representative of the entire school year. This was especially important in Japan, where a national curriculum dictates that different topics be taught at different times of the year across the entire nation. Although we succeeded in videotaping evenly across the school year in the United States and Germany, we were somewhat less successful in Japan, where our sample was skewed toward geometry and away from algebra. For some analyses, therefore, we selected balanced subsamples of algebra and geometry lessons in each country.
Videotaping procedures. At first glance, videotaping classroom instruction seems straightforward: bring in a camera and turn it on. Unfortunately, things are not so simple. Seemingly minor decisions on the part of videographers - such as where to point the camera at any given moment - can significantly affect our view of what is happening in the classroom. To get useful, comparable video in all classrooms, numerous such issues had to be anticipated and resolved in advance.
Standardized procedures for camera use were developed, tested, and revised, and videographers were trained.4 Only one camera was used in each classroom, and it focused on what an ideal student would be focusing on - usually the teacher. After taping, teachers filled out a questionnaire describing the goal of the lesson, its place within the current sequence of lessons, how typical the lesson was, whether they had used methods recommended by the reforms, and so on.
Coding the tapes. When the tapes arrived at our research lab in Los Angeles, they were digitized (to increase durability and random access) and then translated and transcribed. The transcripts were then linked by time codes to the video in a multimedia database. These technical features helped to ease the viewing of the tapes, but they did not help in deciding what to code. Coding classroom instruction is notoriously difficult because there is so much to choose from. We kept two goals in mind: code those aspects that might make a real difference in the mathematics the students were learning, and define codes that would yield valid and informative descriptions of instruction across the three cultures. For the first goal, we drew from the research on teaching and learning in mathematics and from reform documents such as the Professional Standards for Teaching Mathematics.5
To meet the second goal, we convened a team of six code developers, two from each country, and spent the summer of 1994 watching and discussing 27 field-test tapes. Out of these intensive discussions emerged the initial coding system, which included categories such as the nature of the tasks, the kind of work expected of students, and the nature of classroom discourse. The system was refined regularly as the primary coding team began applying it to the actual study tapes and as inter-coder reliability checks indicated that categories needed further definition.
As the coding process unfolded, we found it essential to construct a summary table to represent each lesson. These lesson tables were skeletons of each lesson that showed, on a time-/indexed chart, how the lesson was organized through alternating segments of classwork and seatwork, what pedagogical activities were used (e.g., explaining tasks, demonstrating procedures), what tasks were presented, and the solution strategies for the tasks that were offered by the teacher and the students. Some categories could be coded directly from the tables; some required re-viewing the tapes.
Advantages of video. The benefits of video are well worth the methodological challenges and the labor-intensive demands that this approach imposes. Video provides the researcher with two kinds of data: visual images rich in descriptive power and quantifiable indicators that summarize the contents of large numbers of images. Visual images are vivid and powerful, but they can mislead.6 They can create such a powerful impression that the viewer is seduced into thinking that a single case tells the whole story. Coding relevant indicators enables us to check the representativeness of the images. Each kind of data is significant, and each strengthens the other.
Video data are also relatively raw, in that they are not yet categorized or quantified. Unlike narrative observations or on-site coding, videos have not been filtered through the eyes of individual researchers and are not as constrained by the initial hypotheses of those who design the study. For this reason they can be analyzed by multiple coders with different interests using different coding schemes. We took advantage of this fact by asking a team of four postsecondary mathematics teachers (hereafter, the "Math Group") to analyze the mathematical content of the lessons.
Teaching in Germany, Japan, and the United States
Descriptions of teaching must be selective. There is more going on in a classroom than can be reported, even in a lengthy document. In a brief article, the problem is compounded. What follows is a selection from both the quantitative and qualitative data to illustrate the kind of information the study provides.
What kind of mathematics do students encounter? The nature and level of students' learning are probably influenced by the nature of their mathematical experiences in the classroom. An opening consideration is the kind of mathematics that students in these classrooms encountered. One indicator is how advanced the topics were when compared with their average placement in the mathematics curricula of the 41 TIMSS countries.7 Matched against this scale, the average grade level for lesson topics in the videotape sample was mid-seventh grade for the United States, mid-eighth grade for Germany, and beginning ninth grade for Japan.
For information on the mathematical content students encountered, the Math Group analyzed 15 algebra lessons and 15 geometry lessons randomly selected from each country.8 The group based its analyses on the detailed descriptions of mathematical content contained in the lesson tables described in the previous section. To reduce likelihood of bias, tables were disguised so that it was not possible to tell which country the lessons came from. After analyses were complete, the results were tabulated by country.
One feature on which the team members focused was deductive reasoning, a form of mathematical activity that they considered central for students' engagement in important mathematics. They defined deductive reasoning as the reasoning needed to draw logical conclusions from premises. Mathematical proofs are the most familiar form of such reasoning. Deductive reasoning, as defined by the Math Group, was not common. Only one-fourth of the 90 lessons contained instances of it. As it turned out, these instances were found in 62% of the Japanese lessons, 21% of the German lessons, and 0% of the U.S. lessons.
Together, these indicators suggest that the kind of mathematics studied was significantly different for U.S. students than for their Japanese peers. But this is not the whole story. Perhaps U.S. teachers developed the lower-level content in ways that provided students with rich learning opportunities.
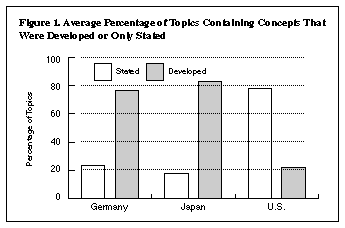
Are mathematical concepts and procedures developed? Mathematical concepts and procedures can either be simply stated by the teacher or be developed through examples, demonstrations, and discussions. Suppose the topic is the area of right triangles. Teachers can state that the area is found by measuring the base, measuring the height, multiplying them together, and dividing the product by 2; demonstrate this procedure for a triangle or two; and then assign problems that enable students to practice the procedure. Alternatively, teachers can develop this procedure, showing, for example, how the formula 12 base x height can be derived by combining two triangles to form a rectangle. Of course, the teacher might ask students to develop some of this themselves. We coded a particular mathematical topic "developed" if teachers made any attempt to motivate a procedure or explain why it worked. As shown in Figure 1, concepts and procedures were usually developed in German and Japanese lessons but merely stated in U.S. lessons.
|
What are students expected to do? In the findings presented thus far, Germany and Japan have appeared more similar to each other than either is to the U.S. When we examine what students actually do during the lessons, however, Germany and Japan diverge. In all three countries, in almost all lessons, students were asked to solve problems. Lessons differed, however, in how much creative mathematical work was expected of the students. In some lessons, a procedure was demonstrated or developed by the teacher, and students then were asked to apply this procedure to solve the assigned problems. In other lessons, students were asked to develop procedures themselves, based on what they had learned in previous lessons.
We coded the nature of the work expected of students during seatwork into three categories: 1) practicing routine procedures, 2) applying procedures in new situations, or 3) inventing new procedures and analyzing new situations. The first category is familiar: the teacher demonstrates or develops a procedure, such as solving a linear equation for x, and then assigns a number of similar problems on which students are to practice the same procedure. The second category includes cases in which a procedure is demonstrated or developed for solving one kind of problem - say, finding the area of a right triangle by adjoining an identical triangle to form a rectangle and calculating half its area. Students are asked to apply the same procedure to another kind of problem, say, finding the areas of nonright triangles. The third category requires even more of students: they are asked to invent solution methods, analyze mathematical situations, or generate mathematical proofs. For example, students might be asked to predict the sum of the interior angles of a 10-sided polygon after measuring the sums for three-, four-, and five-sided polygons.
Coding seatwork into these three categories resulted in the differences shown in Figure 2. Japanese students spent less time practicing routine procedures and more time inventing, analyzing, and proving than their peers in the other countries. German and U.S. students spent almost all their time practicing routine procedures.
What is the teacher's role? Based on the information presented thus far, the reader may have developed the impression that teachers play a far more active role in Germany and the U.S. than in Japan. For example, whereas German and U.S. students usually practice methods developed or presented by the teacher, Japanese students are often asked to develop methods themselves. But to assume that Japanese teachers are less active or directive than German or U.S. teachers would be a mistake.
Although it is true that Japanese teachers give students time to struggle with challenging problems, they often follow this up with direct explanations and summaries of what the students have learned. This is why Japanese teachers were coded as engaging in more direct lecturing than either German or U.S. teachers. Although the time devoted to lecturing was minimal in all three countries, 71% of Japanese lessons contained at least some lecturing, compared with only about 15% of German and U.S. lessons. Japanese teachers also control the direction of the lesson in subtle ways, such as creating conditions in the classroom that will govern the kinds of solution methods students are likely to invent. For example, to begin a lesson, they often select problems that can be solved by modifying methods that were developed during the previous lesson.
How are lessons organized? Even with the small set of indicators presented to this point, it is clear that eighth-grade mathematics teaching differs across countries, especially between Japan and the United States. Students in these classrooms have different mathematical experiences. The differences are not just a matter of degree: U.S. students apparently experience a different kind of mathematics than their Japanese peers. But the indicators don't tell us everything. For example, how do teachers in each country design and implement lessons to produce such clear differences on the indicators?
|
The benefits of video are well worth the methodological challenges and labor-intensive demands that video imposes.
|
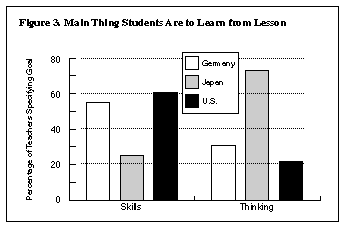
In order to understand how lessons are developed, it is useful to know what goals teachers set. Teachers were asked in the questionnaire what "main thing" they wanted students to learn from the lesson. Most teachers focused either on mathematical skills (solving specific kinds of problems or using specific formulas) or on mathematical thinking (exploring, developing, and understanding mathematical ideas or inventing new ways to solve problems). As shown in Figure 3, there were large differences between countries. Japanese teachers emphasized thinking; German and U.S. teachers emphasized skills. To understand how these goals are translated into classroom lessons, it is helpful to consider the larger context within which they are constructed.
|
We noted earlier that teaching is a cultural activity. Cultural activities often have a "routineness" about them that ensures a degree of consistency and predictability. Lessons are the daily routine of teaching and are usually organized according to a "cultural script," a commonly accepted and predictable way of structuring a classroom session and sequencing the instructional activities. Although we may have a feel for American lessons from our shared experiences, most of us do not know what Japanese lessons look like. For this we need the videos, the visual images.9 Our sense of the scripts that underlie Japanese and American lessons gradually emerged as we watched the videotapes and discussed what we saw with coders and observers from the other countries. The differences in the scripts undoubtedly follow from different instructional goals and are probably based on different assumptions about the nature of mathematics, the ways in which students learn, and the appropriate role for the teacher. Our presentations of these scripts are obviously based on subjective impressions, but their veracity can be checked by other observers and by examining whether they are consistent with the indicator results.
The typical eighth-grade mathematics lesson in the U.S. is organized around two phases: an acquisition phase and an application phase. In the acquisition phase, the teacher demonstrates or leads a discussion on how to solve a sample problem. The aim is to clarify the steps in the procedure so that students will be able to execute the same procedure on their own. In the application phase, students practice using the procedure by solving problems similar to the sample problem. During this seatwork time, the teacher circulates around the room, helping students who are having difficulty. The problems that are not completed by the end of the lesson are often assigned as homework.
The typical eighth-grade mathematics lesson in Japan follows a different script. The lesson focuses on one or sometimes two key problems. After reviewing the major point of the previous lesson and introducing the topic for today's lesson, the teacher presents the first problem. The problem is usually one that students do not know how to solve immediately but for which they have learned some crucial concepts or procedures in their previous lessons. Students are asked to work on the problem for a specified number of minutes and then to share their solutions. The teacher reviews and highlights one or two aspects of the students' solution methods or presents another solution method. Sometimes this cycle is repeated with another problem; other times, students practice the highlighted method or the teacher elaborates it further. Before the lesson ends, the teacher summarizes the major point for the day. Homework is rarely assigned.
Of course, not all teachers in each country teach in these ways, and not all lessons follow these scripts. But what is striking, when viewing the videotapes across the two countries, is how many of the lessons appear consistent with these scripts.
How do teachers view reform? It is interesting to note that in some respects Japanese lessons appear consistent with reform recommendations proposed by such documents as the Professional Standards for Teaching Mathematics of the National Council of Teachers of Mathematics (NCTM). Japanese lessons include high-level mathematics, a clear focus on thinking and problem solving, and an emphasis on students' deriving alternative solution methods and explaining their thinking. In other respects, though, Japanese lessons do not follow such reform guidelines. They include more lecturing and demonstration than even the more traditional U.S. lessons, and we never observed calculators being used in a Japanese classroom.
Regardless of whether Japanese classrooms share features of "reform" classrooms or not, it is quite clear that the typical U.S. classrooms do not. This is especially interesting given the fact that the U.S. teachers, when asked if they were aware of current ideas about the best ways to teach mathematics, responded overwhelmingly in the affirmative. The vast majority reported having read the NCTM standards. Seventy percent of the teachers even claimed to be implementing such ideas in the very lesson that we videotaped. It may be that teachers have changed some features of their instruction and have adopted such reforms as using real-world problems, manipulatives, or cooperative learning. But our data suggest that these changes have not affected the deeper cultural scripts from which teachers work.10 U.S. teachers are still emphasizing the acquisition and application of skills.
| 
