 |




















|
 |
 |
|
author:
|
Daniel I. Rubenstein
|
|
published:
|
03/03/1999
|
|
posted to site:
|
03/03/1999
|
Curiosity and Science
Doing science grows from the childhood processes that we all use everyday, but it matures into something subtly different. Every day, when we don't know something – especially for children in the schools – we ask the ‘if’ question slightly differently. Children don't say ‘if I do this, then such and such should happen.’ Instead they ask if I do this, what will happen?’ This is a subtle, but real difference in the style of questioning.
This difference is what separates the curious child from the scientist. The moving from anything could happen, to a specific prediction about what should happen is what makes a scientist. The ‘what is it, I'm amazed, fascinated, I want to see it,’ to ‘if this happens and I understand how the world works, then I can predict such and such should happen’ is what separates scientists from other curious folk. The trick is for us as teachers to be able to go from unbridled curiosity to the discipline of doing science.
Children, therefore, are budding scientists, but they're not scientists (Figure 5). They're curious and they do all the things that disciplined scientists do. They marvel at the world around them. In fact, they probably marvel at it more than most adults do because, as we get older, we get jaded and put on blinders. We tend to find certain things more interesting than others. To children, everything's equally interesting. So they marvel at everything. And they probe. They're hard to stop probing. If parents say not to do something, they'll do it anyway. They'll test anything, they'll taste anything. They use their senses. They divine information about the world because they're trying to make sense of the unknown.
Unexplained phenomena are not magic to them because they're picking and probing. They're learning. But they are not doing so in the predictive fashion of scientists that I just illustrated. So I'd say children have the ‘right stuff.’ They have all the potential to become scientists, but they're not yet scientists. If we're going to make them scientists, let's examine exactly what a scientist does every moment, every day when they're thinking about the unknowns in the world around them. They're curious and they do all the things that disciplined scientists do. They marvel at the world around them. In fact, they probably marvel at it more than most adults do because, as we get older, we get jaded and put on blinders. We tend to find certain things more interesting than others. To children, everything's equally interesting. So they marvel at everything. And they probe. They're hard to stop probing. If parents say not to do something, they'll do it anyway. They'll test anything, they'll taste anything. They use their senses. They divine information about the world because they're trying to make sense of the unknown.
Unexplained phenomena are not magic to them because they're picking and probing. They're learning. But they are not doing so in the predictive fashion of scientists that I just illustrated. So I'd say children have the ‘right stuff.’ They have all the potential to become scientists, but they're not yet scientists. If we're going to make them scientists, let's examine exactly what a scientist does every moment, every day when they're thinking about the unknowns in the world around them.
What Do Scientists Do?
The first thing scientists do is become interested and fascinated with a phenomenon or a problem they don't understand (Figure 6). It can be something simple that they read in a book. It can be something thrown at them as a question, or it can be something that follows from a previous investigation that they've solved, but that unexpectedly opened up a Pandora's box of other interesting, unexplained phenomena. Ultimately, whatever captivates scientists, they work on. It can be something simple that they read in a book. It can be something thrown at them as a question, or it can be something that follows from a previous investigation that they've solved, but that unexpectedly opened up a Pandora's box of other interesting, unexplained phenomena. Ultimately, whatever captivates scientists, they work on.
Now a lot of people ask if I would work on a particular project. They often offer to pay me to do so! Most times I say ‘no, it's not interesting to me’. I'll only work on problems that I find compelling. And parts of what I find compelling are problems that, if solved, will benefit society at large. So we, as scientists, tackle problems with which we become fascinated. And that’s why there is diversity among scientists and the type of problems they attack.
The first thing we do when we become fascinated with a phenomenon is we start to organize it. We search for a pattern. We identify what we already know and what we do not know about a particular phenomenon. Now this is again where mathematics comes into the process because how else can we see patterns but by organizing data? We often begin by taking measurements, by categorizing, or pigeon-holing our findings. Some examples might be: is the green group different from the red group? Do cold days elicit different responses from hot days? We often use numbers as indices to help us make distinctions. We often plot data as graphs. We reason quantitatively. That's how we find our pattern.
Right at the beginning of an investigation comes the crystallization of apparently strange relationships into patterns that provide some organization. That's the first step. Then we try to find the parts that we don't understand at all. This is what I call identifying the missing pieces. We use intuition, which is essentially our cumulative past experience and knowledge about the world, to help focus our analysis. Such insights can be drawn from book learning, or deductions from the past. They might be ‘facts’ we’ve heard before and that we don't know are really true. But we can use them to organize data.
This wealth of knowledge is our past experience. And it often is what we use intuitively to help pick and probe through the first layers of the problem. It allows scientists to make initial associations. How do we know to ask: is the red group different from the green group? Or that responses to hot days should be different from those of cold days? We learn to ask such questions from the patterns we’ve seen in the past. In doing so, we start to organize the data.
As patterns emerge, some are immediately explainable and we set them aside as solved. Now this is sometimes done at our own peril. This is where the art of science comes in. We may think we understand something by relying on first principles and previous relationships. We may think we've solved a particular part of the problem and put it aside. We are driven to get on with the hard work, the stuff we don't understand. It may turn out that the part of the problem we set aside will lead us down a garden path for five or ten years because our understanding of it was wrong. But until this realization emerges this set aside part of the problem becomes an assumption for the model that we're building.
Scientists use this process of crystallization all the time. It lets us focus on the remaining (unsolved) part of the problem. It's what I call the mental gymnastics of being a scientist. This is the back and forth that scientists enjoy. This starting and stopping, putting problems aside, bringing them back when our understanding doesn’t seem quite right, is a continuous process. A new piece of data may suggest that an old insight was wrong, that our initial intuition was biased, or that a prior relationship was misinterpreted.
Once we start to do this, we're peeling away the problem, like peeling an onion to its core. We're getting down to the nub of the problem that we do not understand. And this is where fun and hard work starts. Now we're at the point where we propose a precise problem and start to ask these magical ‘what if’ questions. By picking and probing, scientists try to ask why something is the way it is. Essentially scientists transform the problems into ‘if-then’ questions: they propose hypotheses with predictions that can be tested.
Once we generate predictions, we test them with experiments or comparisons. The irony is that experimentation or making comparisons is what we do best in the classroom. We teach young children as little scientists, how to do experiments. We teach them what controls are, we teach them how to make comparisons, we teach them how to actually do an investigation. But do we teach them to become fascinated with problems (#1), to search for pattern (#2) and fill in ‘gaps’ by asking ‘what if’ questions (#3)? No, we spend most of our time on point number four.
And then once they have their answers, scientists keep going and probing (#5). We continually worry if we are right, because we never will know for sure. But we keep testing and trying to falsify the answer we have produced. And so we use either confirmatory or disconfirmatory tests. We make further predictions on systems that are very different or where we can change the assumptions. Such experiments or comparisons give us power. If particular predictions are borne out, we begin to believe that we might actually have the right model, the right explanation that transforms the unknown into the known.
A Case Study
This is what scientists do. What I've described is very abstract, so I'm going to share with you one problem that illustrates all the points I've made. The example I will describe is from my own work. I study the behavior of horses, zebras, and wild asses (Figure 7). And I do this in lovely parts of the world. The horses live on a barrier island off of North Carolina. The zebras, as you can imagine, are in Kenya and Tanzania. And the wild asses live in Israel. And as we all know, there are plenty of asses there; both the four legged and the two legged kind!
 Tonight, I will talk about the Asiatic wild ass, also known as the onager. The Palestinian wild ass was driven to extinction by the Ottoman Turks at the turn of the 20th century. One of Israel's goals is to reintroduce into Judaea and Sameria every animal described in the Bible. They've taken the onager from Persia, which is the next closest race, and are rearing them in the Hai-Bar, their breeding farm. They release the onagers into the wilds of Israel. Now Israel can do this because much of Israel is wild and as military training areas they are designated as Nature Reserves. Tonight, I will talk about the Asiatic wild ass, also known as the onager. The Palestinian wild ass was driven to extinction by the Ottoman Turks at the turn of the 20th century. One of Israel's goals is to reintroduce into Judaea and Sameria every animal described in the Bible. They've taken the onager from Persia, which is the next closest race, and are rearing them in the Hai-Bar, their breeding farm. They release the onagers into the wilds of Israel. Now Israel can do this because much of Israel is wild and as military training areas they are designated as Nature Reserves.
Since I'm interested in broad patterns of social behavior, in particular, the evolution of societies, the Israeli government came to me and asked, ‘we are releasing onagers into the Makhtesh Ramm, an erosional crater, but the population is not flourishing. Can you tell us why?’ Between 1983 and 1987, they released a total of nine males and fourteen females into the crater. Most headed back to the Hai-Bar by way of the adjacent Arava Valley which separates Jordan and Israel. At that time, it was mined and most of them were blown up. Since most of the original population was comprised of males the original population would not have grown anyway. Eventually, the Israelis realized that what mattered most was the number of females released because it is females who give birth to offspring that cause populations to grow and determine whether the reintroduction takes hold. They became very troubled by the fact that they released 14 females and ten years later the population contained only 16 breeding females. They wanted to know what was stopping the population from growing.
Slow growth can come about in a variety of ways. First, there could be something limiting birth rate. Second, something could be heightening the death rate. From simple observations--in this uninhabited landscape, where there are plenty of resources -- no onagers were dying. It's clear that slow population growth is not being driven by high death rate. Consequently, we looked at the birth rate. And sure enough, the birth rate was low. We first noted that animals that were released in the wild after being reared in the Hai-Bar, didn't breed as well as those that were reared in the wild. There should have been a lag in the increase in population numbers, but still, after ten years, that can't be the total explanation. Upon closer examination of the data, we noticed that the animals that were being born were all males! This was a surprise and became the puzzle we had to solve if we were going to recommend how to enhance population growth.
Typically, animals in populations will give birth to sons and daughters with equal frequency. We can prove this mathematically, but you can do a thought experiment to see why this must be so. For any sexually dimorphic species where sex is genetically determined, any deviation from a 50:50 ratio makes the rarer sex more valuable. Imagine the case where there are 99 females and one male in a population and each female can give birth to two offspring. If each female is selected to maximize the number of copies of her genes that she spreads into the next generation, what sex offspring should a mother produce if she could control the sex of the offspring she could produce? Obviously, males.
A son can sire offspring from many females and thus provide a female with many grandchildren, whereas a daughter is only going to produce two offspring. In turn each of these daughters would produce two daughters for a total of only 4 grand offspring. And you can do the thought experiment in reverse. Conversely, if daughters are rare, most sons are going to shoot blanks and they're not going to sire any offspring, whereas each daughter is always going to produce two young. As you can see, the only stable point in either case is where 50% of the offspring produced are male and 50% are female. This result emerges because ‘payoffs’ in terms of offspring are frequency dependent.
But we also know from evolutionary theory that there should be exceptions to this rule. If some females can disproportionately control access to resources, then they should produce offspring of the sex that can produce the most grand offspring. As we have seen in polygynous species this sex is male. Thus females that are well endowed, have resources, or are fat, should invest disproportionally in sons. And if their investment helps make her sons among the absolutely best competitors in the population, then those sons will mate multiple times and many grand offspring will be produced. For females that can't invest in sons, because they're emaciated or feeble, they should produce daughters. Daughters will bear at least two offspring whereas, poorly endowed sons, will fail to secure matings and yield no grand-offspring.
So the high risk strategy of producing sons should only be adopted by those females that are well endowed. And the tried and true conservative strategy should be adopted by those females that are less well endowed.
This example of sex ratio control is a fundamental tenet of evolutionary theory and both the general patterns and 'exceptions' have been well studied. Typically the exceptions from a 50:50 ratio occur when individual females can disproportionately control access to resources. Where resources are spatially distributed in clumps and females can use their dominance rank to elbow their way in to clumps of superabundant resources, such dominant females typically produce sons.
But onagers eat grass. And grass, even in a desert where it is sparse to begin with, is fairly homogeneously distributed. So this is a species that shouldn't be exhibiting exceptional sex ratios because no clumps of quality resources are available for disproportionate control. And yet theory actually gives us a way of ‘explaining’ the biased sex ratio. Perhaps age and experience rather than dominance shapes competitive ability and resource acquisition. If so, middle aged females, by virtue of their experience, by their accumulated wisdom, or from the small benefits accumulated in their recent past, might be better endowed than those that are either very young or very old. If this were the case, then we would predict that based on theory, experienced middle-aged females should produce mostly sons.
Thus, we used our understanding of theoretical first principles to generate a hypothesis that makes a very strong prediction that middle aged females should in fact give birth to sons and that primiparous females (first time breeders) and older females should give birth to daughters. Now all we had to do was examine at the data, and determine if sex ratio bias was age dependent.
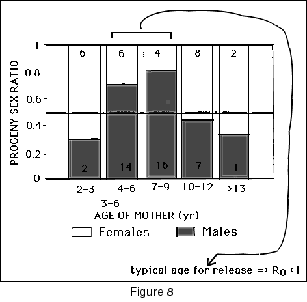 And what we found was, that middle aged females were indeed disproportionately giving birth to sons and that young and old females were disproportionately giving birth to daughters (Figure 8). What was intriguing to note was that the Israelis were biologically sabotaging their reintroductions while behaving as cost effective and rational managers! When they were moving animals from the Hai-Bar to the crater, they didn't move youngsters who were inexperienced and who had a high probability of dying. And they didn't move oldsters who didn't have much life left to live. They moved middle aged females in their prime. And what did those middle-aged females do? They bore sons, and the population stopped growing! And what we found was, that middle aged females were indeed disproportionately giving birth to sons and that young and old females were disproportionately giving birth to daughters (Figure 8). What was intriguing to note was that the Israelis were biologically sabotaging their reintroductions while behaving as cost effective and rational managers! When they were moving animals from the Hai-Bar to the crater, they didn't move youngsters who were inexperienced and who had a high probability of dying. And they didn't move oldsters who didn't have much life left to live. They moved middle aged females in their prime. And what did those middle-aged females do? They bore sons, and the population stopped growing!
This example shows that we were able to solve the problem using our intuition and our past experience, and then drawing on a piece of evolutionary theory which normally doesn't find its way into management and conservation decision-making, to generate an hypothesis with a prediction which could be tested by re-evaluating the original data. The Israelis were behaving as rational managers, but based on our scientific analysis we suggested that they change their ways. We told them to select older females, who are going to give birth to daughters, and whose daughters as young first-time breeders were also going to give birth to daughters and to reintroduce such pairs. By doing so female births should increase multiplicatively and inject a large cohort of females in to the population. This recommendation has proved to be so successful that the Israelis are using this strategy for other reintroductions and these populations are also growing nicely.
So here's a case of using the scientific method in ways that really illuminate how a scientist thinks. We became fascinated with this problem. We solved and set aside the easy part, the low birth rate as a possible result of increased mortality, and then we drew upon ideas we remembered from our past, ideas derived from basic evolutionary theory. The use of theory represents a critical link to disciplinary content. The connection with theory allowed us to fill in the gaps by extending the theory. We then posed a precise problem in the form of an ‘if-then’ question. Finally, we tested our prediction by re-examining the existing data, but in a novel way.
But we weren’t finished. We kept probing. We knew our hypothesis accounted for the Israeli population, but how general was it? To ascertain generality we called all the zoos that raised onagers and got their breeding records. And, sure enough, exactly the same pattern emerged. In the end we performed a confirmatory test.
 This example illustrates how a scientist does science. And as you see, a scientist is using the traditional scientific method of discovery, hypothesis generation, and then hypothesis testing (Figure 9). But if you look carefully, the method was not applied in linear fashion. We peeled away problems, we looked at many alternative simple problems, and then we reevaluated the completeness of our understanding based on the model we constructed. This example illustrates how a scientist does science. And as you see, a scientist is using the traditional scientific method of discovery, hypothesis generation, and then hypothesis testing (Figure 9). But if you look carefully, the method was not applied in linear fashion. We peeled away problems, we looked at many alternative simple problems, and then we reevaluated the completeness of our understanding based on the model we constructed.
|
 |

