Conference Material

An emerging profile of the mathematical achievement of students in the Core-Plus mathematics project

In addition to geometry and algebra strands, CPMP's curriculum also includes statistics, probability, and discrete mathematics. CPMP students were assessed on these two strands on the CPMP Posttest Part 2 for each course. Since comparison students would have little opportunity to learn this content, they did not complete part 2 of these posttests. An example of a discrete mathematics assessment item from Course 2 Posttest Part 2 is given in Figure 7. CPMP students' achievement level in statistics and probability is discussed later.

Assessment Setting

For a time in the nineteenth century, a Pony Express mail system was used in some of the great plains states. Mail routes between towns were given a rating depending on distance, difficulty, and time. Five towns on the Pony Express system are St. Joseph (S), Omaha˙(O), Denver˙(D), Oklahoma City (K), and Dodge City (G). This diagram illustrates the mail routes between pairs of these towns and the rating of each.

Task	CPMP Mean (SD)
(a). The lower the total rating, the "better" a route. What is the best route from St. Joseph to Denver? What is its rating? Explain your reasoning.	2.6 (1.2)
(b). A presidential candidate used the mail route ratings to plan a campaign trip from St. Joseph to each town and then back to St. Joseph. On the copy of the network below darken a route for the campaign trip that has the lowest total rating. What is the total rating of the route?	3.3 (1.1)
(c). This mail system soon proved to be very expensive. In order to economize, the U.S. Postal Service decided to streamline the system. They continued to operate only those routes that allowed mail to get to every town once in such a way that the total rating was minimum. On the right, darken the edges of a network that will satisfy these conditions.	2.6 (1.2)

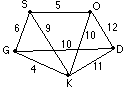
Figure 7. Discrete Mathematics task from the Course 2 Posttest Part 2

This task is based on content found in the Course 2 unit, "Network Optimization." Parts (a) and (b) involve calculating and comparing ratings for various routes. Part (c) requires a minimal spanning tree for this network. Means on the 0 - 4 rubric suggest that most CPMP students understood the tasks and completed them successfully.

NAEP-based Test The National Assessment of Educational Progress (NAEP) is administered periodically as a means of monitoring U. S. students' achievement levels in various subject areas. In 1990 and 1992, a NAEP mathematics assessment was administered at several grade levels, including grade 12. As another measure of CPMP students' achievement, a 30-item test was constructed with balance among the five content (numbers & operations; measurement; geometry; data, statistics & probability; and algebra & functions) and three process categories (concepts, problem solving, and procedures). The NAEP subtest and item results are another component of the emerging profile of CPMP students' achievement.

The NAEP-based test was administered in May 1997 to CPMP students at the end of Course 3. A total of 1,292 students in 23 CPMP field test schools completed this test. The students in these schools were generally representative of all CPMP students in the field test at the end of Course 3. For example, the students in these 22 schools who took both the Course 1 ATDQT pretest and the Course 3 ATDQT posttest had a mean of 270.35 and standard deviation of 35.81 on the Course 1 pretest, which is very close to the mean of 267.79 and standard deviation of 35.77 for all students in the field test schools.

The items were part of the NAEP assessment of twelfth-grade students in October of either 1990 or 1992. According to Kenney & Silver (1997), the 1992 NAEP sample consisted of 8,499 students that were representative of all twelfth graders in the country. One important descriptor of 1992 twelfth-grade students, from which the NAEP sample was drawn, is the highest level of mathematics course taken in high school. This data, taken from school transcripts, is given in Figure 8.

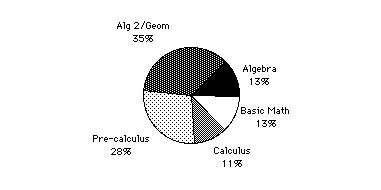Figure 8. Percent of 1992 students completing various high school courses (Rock & Pollack, 1995)

On the 30-item NAEP-based CPMP test, the mean of the national sample was 12.8 (42.7%). The Course 3 students' mean was 16.9 (56.4%) with standard deviation of 5.36. This difference in overall means is large (about 0.77 standard deviations), but no assurance can be given of the comparability of the two groups' mathematical aptitudes and backgrounds. (The 30-item NAEP-based test had a KR-20 reliability of 0.82 when administered to the CPMP sample.) Rather than focus on comparing means of the NAEP sample with those of the Course 3 students, the item data from the NAEP sample is used as a benchmark of the difficulty of an item or of all items in a content or process category. This approach allows for meaningful between-item and between-category comparisons of Course 3 students' results.

Given the large difference in overall group means, it is not surprising that the Course 3 students scored considerably higher than the NAEP sample in all content and process categories. However, the magnitude of the differences varied among categories, and it seems reasonable to assume that the larger the difference in means in a category, the better the relative performance of the CPMP students. Figure 9 illustrates the mean percent correct in each content and process category for the Course 3 students and for the NAEP sample. Content and process categories appear in descending order of the difference between the two mean percents.

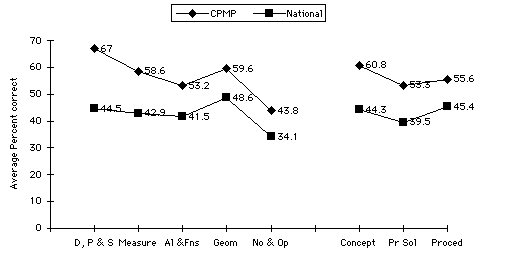Content Subtest Process Subtest

Figure 9. Percent correct on each NAEP subtest for CPMP and NAEP twelfth-grade sample

Of the process categories, CPMP students' performance relative to the NAEP sample was best on conceptual items followed by problem solving and finally by items in the procedural category. This outcome is consistent with CPMP's emphasis on sense making, on applications and on problem solving with an accompanying de-emphasis on procedural skill practice. Although the following presentation of results is organized by content categories, NAEP's process categorization of each sample item is also provided.

Content Categories Of the five content categories, the Course 3 students scored highest on data analysis, statistics and probability, a strand of the CPMP curriculum that is not emphasized in most of the more traditional mathematics curricula. Three of the four items in this content category were classified by NAEP as conceptual and one as problem solving. All four items are given in Figure 10.

Data Analysis, Statistics and Probability Item	CPMP	NAEP
[Conceptual] A certain company keeps a list of 50 employees and their annual salaries. When the salary of the very highly paid president is added to this list, which of the following statistics is most likely to be approximately the same or nearly the same for the original list and the new list? (a) The highest salary (b) The range (c) The mean *(d) The median (e) The standard deviation	44%	21%
[Problem Solving] From a shipment of 500 batteries, a sample of 25 was selected at random and tested. If 2 batteries in the sample were found to be dead, how many dead batteries would be expected to be in the sample? (a) 10 (b) 20 (c) 30 *(d) 40 (e) 50	80%	51%
[Conceptual] The total distances covered by two runners during the first 28 minutes of a race are shown in the graph above. How long after the start of the race did one runner pass the other? (a) 3 minutes (b) 8 minutes (c) 12 minutes *(d) 14 minutes (e) 28 minutes	93%	75%
[Conceptual] In the graph above, each dot shows the number of sit-ups and the corresponding age for one of 13 people. According to this graph, what is the median number of sit-ups for these 13 people? (a) 15 (b) 20 (c) 45 *(d) 50 (e) 55	51%	31%

Figure 10. Sample data analysis, statistics and probability items

On the first item, CPMP students showed an understanding of statistical concepts like mean, median, range and standard deviation well beyond the level of the NAEP twelfth-grade sample. On the second item, 80% of CPMP students were able to solve a problem involving the idea of sampling. The third item simply requires reading a graph, which 93% of CPMP students were able to do. The fourth item requires an understanding of a scatterplot and the concept of median. CPMP students performed particularly well on the third and fourth items as they consistently do on tasks that assess interpretation of information presented graphically.

Second to data analysis, statistics and probability, CPMP students performed especially well on measurement items. The eight items in the measurement category assessed students' understanding of and ability to apply various measurement topics including the volume of a right circular cylinder, volume of a rectangular prism, perimeter and area of a rectangle and square, and area and circumference of a circle. Six of these items are classified as problem solving and two as procedural. Differences in percent correct on the eight items for CPMP students compared to the NAEP twelfth-grade sample ranged from 6% to 27%, all higher for the CPMP students. Four measurement items are given in Figure 11, including the ones with the greatest and least performance difference and one that is classified by NAEP as procedural.

Measurement Time	CPMP	NAEP
[Problem Solving] The perimeter of a square is 24 centimeters. What is the area of the square? *(a) 36 cm2 (b) 48 cm2 (c) 96 cm2 (d) 576 cm2 (e) I don't know	66%	45%
[Problem Solving] A rectangular pool 24 feet long, 8 feet wide, and 4 feet deep is filled with water. Water is leaking from the pool at the rate of 0.40 cubic foot per minute. At this rate, how many hours will it take for the water level to drop 1 foot? (a) 4 *(b) 8 (c) 12 (d) 16 (e) 32	32%	26%
[Problem Solving] In the figure above, a circle with center O and radius of length 3 is inscribed in a square. What is the area of the shaded region? (a) 3.86 *(b) 7.73 (c) 28.27 (d) 32.86 (e) 36.00	64%	37%
BR> [Procedural] The volume V of a right circular cylinder like the one in the figure above is given by the formula V = *r2h. In terms of *, what is the volume of a cylinder with radius r= 4 and height h = 10? (a) 18* (b) 26* (c) 80* *(d) 160* (e) 1,600*	84%	68%

Figure 11. Sample measurement items

On the six items that NAEP classified as algebra & functions, CPMP students averaged 11.7% higher than the twelfth-grade NAEP sample, third among the five content categories. Specific content in this category included evaluating an algebraic expression for a given value of x, finding the cosine of an angle, finding the length of an altitude of a right triangle using trigonometry, solving an exponential equation, and using a given "if-then" statement to determine which of several statements cannot be true. Three of these items were classified as conceptual, two as procedural and one as problem solving. Two of the procedural items, a conceptual item, and a problem solving item are given in Figure 12. Again, the item performance differences in favor of the CPMP students were less on the procedural items than on those classified as conceptual or problem-solving, as was the case for the entire test.

Algebra and Functiona Items	CPMP	NAEP
[Problem Solving] The following statement is true: "If Sally goes to the movie, Mark will go also." Which statement below could NOT be true? (a) Sally and Mark both go to the movie. *(b) Sally goes to the movie and Mark does not go. (c) Mark goes to the movie and Sally does not go. (d) Neither Mark nor Sally goes to the movie. (e) I don't know.	63%	51%
[Conceptual] For what value of x is 812 = 16x ? (a) 3 (b) 4 (c) 8 *(d) 9 (e) 12	82%	34%
[Procedural) If x = -4, the value of -4x is (a) -16 (b) -8 (c) 8 *(d) 16	83%	75%
[Procedural] In right triangle ABC above, cos A = *(a) 3/5 (b) 3/4 (c) 4/5 (d) 4/3 (e) 5/3	34%	30%

Figure 12. Sample algebra & functions items

The NAEP twelfth-grade sample scored higher than the CPMP students on only two of the 30 items on the test. One of those items was in the algebra & functions category. In that item, students were to identify a given graph as x*y from among choices x * y, x < y and x > y. Just 35% of CPMP students and 36% of NAEP twelfth graders responded correctly. A partial explanation for the relatively poor performance of CPMP students on this item may be that the curriculum emphasizes a function approach. Thus, CPMP students usually worked with inequalities in which y was on the left and f(x) was on the right.

On the seven geometry items, the CPMP students average percent correct was 11.0 percentage points higher than that of the NAEP twelfth graders. Three of the seven geometry items were classified as conceptual, two as procedural, and two as problem solving. Two conceptual, one procedural and one problem solving geometry item are given in Figure 13.

Geometry Item	CPMP	NAEP
[Conceptual] Which of the following is NOT a property of every rectangle? (a) The opposite sides are equal in length. (b) The opposite sides are parallel. (c) All angles are equal in measure. *(d) All sides are equal in length. (e) The diagonals are equal in length.	86%	71%
[Conceptual] The length of a side of the square above is 6. What is the length of the radius of the circle? (a) 2 *(b) 3 (c) 4 (d) 6 (e) 8	83%	70%
[Procedural) What is the slope of the line shown in the graph above? (a) 1/3 *(b) 2/3 (c) 1 (d) 3/2 (e) 3	47%	41%
Problem Solving In the xy-plane, a line parallel to the x-axis intersects the y-axis at the point (0, 4). This line also intersects a circle in two points. The circle has a radius of 5 and its center is at the origin. What are the coordinates of the two points of intersection? (a) (1, 2) and (2, 1) (b) (2, 1) and (2, -1) (c) (3, 4) and (3, -4) *(d) (3, 4) and (-3, 4) (e) (5, 0) and (-5, 0)	44%	32%

Figure 13. Sample geometry items

Specific content of the seven geometry items included identifying properties of a rectangle, finding the slope of a line given the coordinates of two of its points, finding the distance between two points with given coordinates, finding the points of intersection of a line and a circle, finding the measure of the angle formed by the bisectors of two adjacent angles, finding the length of the side of a square from the radius of the inscribed circle, and applying the fact that a parallelogram is formed whenever the midpoints of a quadrilateral are joined in succession.

The five items that were categorized as numbers & operations assessed percent, ratio and proportion, and operations with integers. For the most part, these topics are assumed and used in applications in both the CPMP and the traditional high school curricula for college-intending students but not taught as new content. One topic in this category that is taught in both curricula is exponential growth including compound interest. Of the five items in the numbers & operations category, two were classified as conceptual, two as procedural, and one as problem solving. One item of each process type is given in Figure 14. As these items exemplify, number & operations was the most difficult of the five content categories with CPMP students averaging 43.7% correct compared to just 34.1% for the NAEP twelfth graders.

Number and Operations Line	CPMP	NAEP
[Conceptual] Suppose 4t = 3s = 10t, where r, s, and t are positive integers. What is the sum of the least values of r, s, and t for which this equality is true? (a) 7 (b) 17 *(c) 41 (d) 82 (e) 120	41%	30%
[Procedural) A savings account earns 1 percent per month on the sum of the initial amount deposited plus any accumulated interest. If a savings account is opened with an initial deposit of $1,000 and no other deposits or withdrawals are made, what will be the amount in this account at the end of 6 months? (a) $1,060.00 *(b) $1,061.52 (c) $1,072.14 (d) $1,600.00 (e) $6,000.00	36%	15%
(Problem Solving) It takes 28 minutes for a certain bacteria population to double. If there are 5,241,763 bacteria in this population at 1:00 p.m., which of the following is closest to the number of bacteria in millions at 2:30 p.m. on the same day? (a) 80 *(b) 40 (c) 20 (d) 15 (e) 10	41%	31%

Figure 14. Sample number & operations items

The second of two items in which CPMP students had a lower percent correct than the NAEP twelfth-grade sample was a number & operations item. The stem of this item read "In a group of 1,200 adults, there are 300 vegetarians. What is the ratio of nonvegetarians to vegetarians in the group?" Only 25% of NAEP twelfth graders and 21% of Course 3 students chose the correct response, "3 to 1." More CPMP students were attracted to "4 to 1" (36.7%) and "1 to 4" (31.2%) than to the keyed answer. A partial explanation for the poor performance of students on this item may lie in its specialized wording, which is likely to be used when students are first learning the ratio concept (that is, in middle school) but is rarely encountered in more realistic or mathematically advanced settings. This item was also one of the four poorest discriminating items for CPMP students with a discrimination /index (biserial correlation of scores on the item with scores on all 30 items) of 0.27 compared to a mean item discrimination /index of 0.40 across all 30 items.

In this section, we summarize the findings to date with respect to mathematical achievement of CPMP students on various criterion measures. The first set of findings are based on ATDQT test forms as criterion measures.

• When school means are the statistical unit, CPMP students' posttest means (adjusted for pretest differences) were greater than those of a comparison group of students enrolled in traditional mathematics curricula at the end of both Course 1 (p = .086) and Course 2 (p = .027).

• Whether aggregated student scores or school means are the statistical unit, CPMP students' posttest means at the end of Courses 1, 2, and 3 were greater than those of the national test norm group at the same pretest levels.

• With the exception of urban schools at the end of Course 1, the posttest means of CPMP students in rural, urban and suburban schools in Courses 1, 2, and 3 were greater than those of the national norm group at the same pretest levels.

• In five categories of CPMP class make-up (all students, wide range but none of the very top, wide range but not the very top or very bottom, college-intending only, and work-prep only), the posttest means of the CPMP students in Courses 1, 2, and 3 were greater than those of the national norm group at the same pretest levels. One exception was the work-prep only group at the end of Course 1.

• In all three course cohorts, the posttest means of females and the posttest means of males in CPMP were both greater than those of the national norm group at the same pretest levels. Females grew slightly more than males in each CPMP cohort group, but none of the gender differences were statistically significant.

• In Courses 1, 2, and 3, the posttest means of CPMP students whose first language was not English were greater than those of the national norm group at the same pretest levels.

• In Courses 1, 2, and 3, the posttest means of CPMP students in all minority groups (African Americans, Asian Americans, Hispanics, and Native/Alaskan Americans) were greater than those of the national norm group at the same pretest levels. Hispanics made the greatest pretest to posttest gains at the end of each course.

• The Course 1 Posttest mean of CPMP students in a Mathematics and Science Center was about double that of the national norm group at the same pretest level. (This group's median pretest score was at the 97th national percentile.)

• CPMP students scored significantly higher than comparison students on subtests of algebraic concepts (Courses 1 and 2) and of geometric concepts (Course 2).

• At the end of Course 1, comparison students scored higher than CPMP students on a subtest of algebraic procedures, but the CPMP mean was slightly higher than the comparison mean at the end of Course 2.

• CPMP students also illustrated an understanding of statistics and probability topics (e.g. centers and variability of distributions, various ways to display and interpret data graphically, simulation, and expected values in Course 1 and correlation, least squares regression, waiting time distributions, independent events, and fair price in Course 2) and of discrete mathematics topics (e.g. Euler paths, critical paths, and graph coloring in Course 1 and minimal spanning trees and matrices in Course˙2).