Paper

Understanding and Improving Classroom Mathematics Instruction: An Overview of the TIMSS Video Study

Collecting national samples of teaching can serve two important purposes. First, it gives us solid information about the processes of teaching and learning inside U.S. classrooms, information that is crucial for developing sound education policies. Efforts to improve student learning succeed or fail inside the classroom, a fact that has too often been ignored by would-be reformers. Setting standards for content and performance is an important first step. But student learning will not be improved merely by setting standards and holding teachers accountable. We must study directly the processes that lead to learning in the classroom, for if we do not understand these processes we will have little chance of improving them. Most other professional and industrial fields have determined that improving the quality of the processes is the surest road to improving products, but we in education have yet to learn this lesson. The videotape study of classroom instruction allows us to refocus on teaching processes, with the aim of improving students' learning.

National samples of teaching also enable us to compare U.S. teaching methods with those used in other countries. This comparison allows us to see teaching in a new way. Teaching is a cultural activity.1 It is an everyday event that occurs throughout all parts of American society. Over time, we have developed norms and expectations for teaching that are widely shared and passed along as one generation of students becomes the next generation of teachers.2 Because our models of how teaching should look are so widely shared and so familiar, they become nearly invisible. We come to believe that this is the way teaching must be. When we observe teaching in other countries, these accepted and unquestioned practices are brought to light, and we see that we teach the way we do because we choose to teach this way. This realization is crucial because it opens up new possibilities for how we might improve teaching.

Conducting the TIMSS Video Study

U.S. students performed poorly in the Second International Mathematics Study (SIMS), conducted in the 1980s. Consequently, as planning commenced for the TIMSS, there was great interest in being able to go beyond the cross-national achievement data to focus on the underlying processes that produce achievement. Instructional processes in the classroom were assumed to be an important cause of student learning. But how could something as complex as teaching be studied on a large scale, across cultures?

One approach is to give teachers a questionnaire asking them to describe their instructional practices. Although such a questionnaire had been administered as part of SIMS, there are problems with this approach. Even within the U.S., we lack shared meanings for the words we use to describe teaching. One teacher will call something "problem solving" while her colleague next door calls the same thing a "routine exercise." The problem of no shared language is compounded in a cross-cultural questionnaire study. The responses are nearly impossible to interpret.

Thus the decision was made to collect direct information on teaching by videotaping classroom instruction. Video had long been used for small-scale, in-depth qualitative research but had never been employed on such a large scale before. For this reason, the scope of the study was limited to one of the three grade levels studied in TIMSS (eighth grade) and to three of the 41 TIMSS countries (Germany, Japan, and the United States). Germany and Japan were chosen because they are both viewed as important economic competitors of the U.S. Japan is of special interest because it has repeatedly scored near the top in international comparisons of mathematics achievement.

Three straightforward goals guided the study: 1) to learn how eighth-grade mathematics is taught in the United States, 2) to learn how eighth-grade mathematics is taught in the two comparison countries, and 3) to learn how American teachers view reform and to see whether they are implementing teaching reforms in their classrooms. To achieve these goals, a number of methodological hurdles had to be cleared.

Sampling. If we wanted to use video to paint national portraits of eighth-grade mathematics instruction, we needed to be sure that the videotapes we analyzed were representative of instruction in each country. A number of issues were considered. First, how should classrooms be selected? Fortunately, the TIMSS sampling plan was highly sophisticated. For this reason, it was possible to construct the video sample as a random subsample of the full TIMSS sample.3 Not only were specific teachers selected, but specific class periods as well. No substitutions were allowed, either by another teacher within the same school or by another class period with the same teacher. The final video sample included 231 classrooms: 100 in Germany, 50 in Japan, and 81 in the United States.

Having chosen the classrooms, we next needed to decide how many lessons to videotape in each one. In the end, we videotaped one lesson in each classroom. Although this enabled us to study the largest number of teachers within our budget, it precluded our studying some important parts of the teaching process, such as the methods teachers use for linking lessons together into units.

Finally, we wanted to be sure that our sample was representative of the entire school year. This was especially important in Japan, where a national curriculum dictates that different topics be taught at different times of the year across the entire nation. Although we succeeded in videotaping evenly across the school year in the United States and Germany, we were somewhat less successful in Japan, where our sample was skewed toward geometry and away from algebra. For some analyses, therefore, we selected balanced subsamples of algebra and geometry lessons in each country.

Videotaping procedures. At first glance, videotaping classroom instruction seems straightforward: bring in a camera and turn it on. Unfortunately, things are not so simple. Seemingly minor decisions on the part of videographers - such as where to point the camera at any given moment - can significantly affect our view of what is happening in the classroom. To get useful, comparable video in all classrooms, numerous such issues had to be anticipated and resolved in advance.

Standardized procedures for camera use were developed, tested, and revised, and videographers were trained.4 Only one camera was used in each classroom, and it focused on what an ideal student would be focusing on - usually the teacher. After taping, teachers filled out a questionnaire describing the goal of the lesson, its place within the current sequence of lessons, how typical the lesson was, whether they had used methods recommended by the reforms, and so on.

Coding the tapes. When the tapes arrived at our research lab in Los Angeles, they were digitized (to increase durability and random access) and then translated and transcribed. The transcripts were then linked by time codes to the video in a multimedia database. These technical features helped to ease the viewing of the tapes, but they did not help in deciding what to code. Coding classroom instruction is notoriously difficult because there is so much to choose from. We kept two goals in mind: code those aspects that might make a real difference in the mathematics the students were learning, and define codes that would yield valid and informative descriptions of instruction across the three cultures. For the first goal, we drew from the research on teaching and learning in mathematics and from reform documents such as the Professional Standards for Teaching Mathematics.5

To meet the second goal, we convened a team of six code developers, two from each country, and spent the summer of 1994 watching and discussing 27 field-test tapes. Out of these intensive discussions emerged the initial coding system, which included categories such as the nature of the tasks, the kind of work expected of students, and the nature of classroom discourse. The system was refined regularly as the primary coding team began applying it to the actual study tapes and as inter-coder reliability checks indicated that categories needed further definition.

As the coding process unfolded, we found it essential to construct a summary table to represent each lesson. These lesson tables were skeletons of each lesson that showed, on a time-indexed chart, how the lesson was organized through alternating segments of classwork and seatwork, what pedagogical activities were used (e.g., explaining tasks, demonstrating procedures), what tasks were presented, and the solution strategies for the tasks that were offered by the teacher and the students. Some categories could be coded directly from the tables; some required re-viewing the tapes.

Advantages of video. The benefits of video are well worth the methodological challenges and the labor-intensive demands that this approach imposes. Video provides the researcher with two kinds of data: visual images rich in descriptive power and quantifiable indicators that summarize the contents of large numbers of images. Visual images are vivid and powerful, but they can mislead.6 They can create such a powerful impression that the viewer is seduced into thinking that a single case tells the whole story. Coding relevant indicators enables us to check the representativeness of the images. Each kind of data is significant, and each strengthens the other.

Video data are also relatively raw, in that they are not yet categorized or quantified. Unlike narrative observations or on-site coding, videos have not been filtered through the eyes of individual researchers and are not as constrained by the initial hypotheses of those who design the study. For this reason they can be analyzed by multiple coders with different interests using different coding schemes. We took advantage of this fact by asking a team of four postsecondary mathematics teachers (hereafter, the "Math Group") to analyze the mathematical content of the lessons.

Teaching in Germany, Japan, and the United States

Descriptions of teaching must be selective. There is more going on in a classroom than can be reported, even in a lengthy document. In a brief article, the problem is compounded. What follows is a selection from both the quantitative and qualitative data to illustrate the kind of information the study provides.

What kind of mathematics do students encounter? The nature and level of students' learning are probably influenced by the nature of their mathematical experiences in the classroom. An opening consideration is the kind of mathematics that students in these classrooms encountered. One indicator is how advanced the topics were when compared with their average placement in the mathematics curricula of the 41 TIMSS countries.7 Matched against this scale, the average grade level for lesson topics in the videotape sample was mid-seventh grade for the United States, mid-eighth grade for Germany, and beginning ninth grade for Japan.

For information on the mathematical content students encountered, the Math Group analyzed 15 algebra lessons and 15 geometry lessons randomly selected from each country.8 The group based its analyses on the detailed descriptions of mathematical content contained in the lesson tables described in the previous section. To reduce likelihood of bias, tables were disguised so that it was not possible to tell which country the lessons came from. After analyses were complete, the results were tabulated by country.

One feature on which the team members focused was deductive reasoning, a form of mathematical activity that they considered central for students' engagement in important mathematics. They defined deductive reasoning as the reasoning needed to draw logical conclusions from premises. Mathematical proofs are the most familiar form of such reasoning. Deductive reasoning, as defined by the Math Group, was not common. Only one-fourth of the 90 lessons contained instances of it. As it turned out, these instances were found in 62% of the Japanese lessons, 21% of the German lessons, and 0% of the U.S. lessons.

Together, these indicators suggest that the kind of mathematics studied was significantly different for U.S. students than for their Japanese peers. But this is not the whole story. Perhaps U.S. teachers developed the lower-level content in ways that provided students with rich learning opportunities.

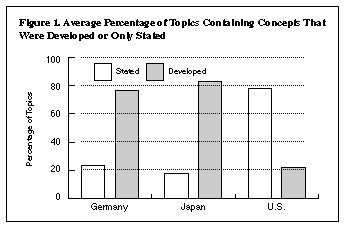
Are mathematical concepts and procedures developed? Mathematical concepts and procedures can either be simply stated by the teacher or be developed through examples, demonstrations, and discussions. Suppose the topic is the area of right triangles. Teachers can state that the area is found by measuring the base, measuring the height, multiplying them together, and dividing the product by 2; demonstrate this procedure for a triangle or two; and then assign problems that enable students to practice the procedure. Alternatively, teachers can develop this procedure, showing, for example, how the formula 12 base x height can be derived by combining two triangles to form a rectangle. Of course, the teacher might ask students to develop some of this themselves. We coded a particular mathematical topic "developed" if teachers made any attempt to motivate a procedure or explain why it worked. As shown in Figure 1, concepts and procedures were usually developed in German and Japanese lessons but merely stated in U.S. lessons.

What are students expected to do? In the findings presented thus far, Germany and Japan have appeared more similar to each other than either is to the U.S. When we examine what students actually do during the lessons, however, Germany and Japan diverge. In all three countries, in almost all lessons, students were asked to solve problems. Lessons differed, however, in how much creative mathematical work was expected of the students. In some lessons, a procedure was demonstrated or developed by the teacher, and students then were asked to apply this procedure to solve the assigned problems. In other lessons, students were asked to develop procedures themselves, based on what they had learned in previous lessons.

We coded the nature of the work expected of students during seatwork into three categories: 1) practicing routine procedures, 2) applying procedures in new situations, or 3) inventing new procedures and analyzing new situations. The first category is familiar: the teacher demonstrates or develops a procedure, such as solving a linear equation for x, and then assigns a number of similar problems on which students are to practice the same procedure. The second category includes cases in which a procedure is demonstrated or developed for solving one kind of problem - say, finding the area of a right triangle by adjoining an identical triangle to form a rectangle and calculating half its area. Students are asked to apply the same procedure to another kind of problem, say, finding the areas of nonright triangles. The third category requires even more of students: they are asked to invent solution methods, analyze mathematical situations, or generate mathematical proofs. For example, students might be asked to predict the sum of the interior angles of a 10-sided polygon after measuring the sums for three-, four-, and five-sided polygons.

Coding seatwork into these three categories resulted in the differences shown in Figure 2. Japanese students spent less time practicing routine procedures and more time inventing, analyzing, and proving than their peers in the other countries. German and U.S. students spent almost all their time practicing routine procedures.

What is the teacher's role? Based on the information presented thus far, the reader may have developed the impression that teachers play a far more active role in Germany and the U.S. than in Japan. For example, whereas German and U.S. students usually practice methods developed or presented by the teacher, Japanese students are often asked to develop methods themselves. But to assume that Japanese teachers are less active or directive than German or U.S. teachers would be a mistake.

Although it is true that Japanese teachers give students time to struggle with challenging problems, they often follow this up with direct explanations and summaries of what the students have learned. This is why Japanese teachers were coded as engaging in more direct lecturing than either German or U.S. teachers. Although the time devoted to lecturing was minimal in all three countries, 71% of Japanese lessons contained at least some lecturing, compared with only about 15% of German and U.S. lessons. Japanese teachers also control the direction of the lesson in subtle ways, such as creating conditions in the classroom that will govern the kinds of solution methods students are likely to invent. For example, to begin a lesson, they often select problems that can be solved by modifying methods that were developed during the previous lesson.

How are lessons organized? Even with the small set of indicators presented to this point, it is clear that eighth-grade mathematics teaching differs across countries, especially between Japan and the United States. Students in these classrooms have different mathematical experiences. The differences are not just a matter of degree: U.S. students apparently experience a different kind of mathematics than their Japanese peers. But the indicators don't tell us everything. For example, how do teachers in each country design and implement lessons to produce such clear differences on the indicators?

The benefits of video are well worth the methodological challenges and labor-intensive demands that video imposes.

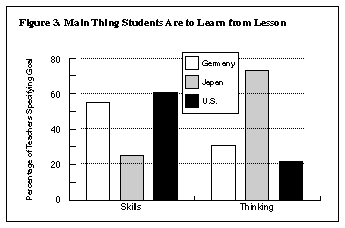
In order to understand how lessons are developed, it is useful to know what goals teachers set. Teachers were asked in the questionnaire what "main thing" they wanted students to learn from the lesson. Most teachers focused either on mathematical skills (solving specific kinds of problems or using specific formulas) or on mathematical thinking (exploring, developing, and understanding mathematical ideas or inventing new ways to solve problems). As shown in Figure 3, there were large differences between countries. Japanese teachers emphasized thinking; German and U.S. teachers emphasized skills. To understand how these goals are translated into classroom lessons, it is helpful to consider the larger context within which they are constructed.

We noted earlier that teaching is a cultural activity. Cultural activities often have a "routineness" about them that ensures a degree of consistency and predictability. Lessons are the daily routine of teaching and are usually organized according to a "cultural script," a commonly accepted and predictable way of structuring a classroom session and sequencing the instructional activities. Although we may have a feel for American lessons from our shared experiences, most of us do not know what Japanese lessons look like. For this we need the videos, the visual images.9 Our sense of the scripts that underlie Japanese and American lessons gradually emerged as we watched the videotapes and discussed what we saw with coders and observers from the other countries. The differences in the scripts undoubtedly follow from different instructional goals and are probably based on different assumptions about the nature of mathematics, the ways in which students learn, and the appropriate role for the teacher. Our presentations of these scripts are obviously based on subjective impressions, but their veracity can be checked by other observers and by examining whether they are consistent with the indicator results.

The typical eighth-grade mathematics lesson in the U.S. is organized around two phases: an acquisition phase and an application phase. In the acquisition phase, the teacher demonstrates or leads a discussion on how to solve a sample problem. The aim is to clarify the steps in the procedure so that students will be able to execute the same procedure on their own. In the application phase, students practice using the procedure by solving problems similar to the sample problem. During this seatwork time, the teacher circulates around the room, helping students who are having difficulty. The problems that are not completed by the end of the lesson are often assigned as homework.

The typical eighth-grade mathematics lesson in Japan follows a different script. The lesson focuses on one or sometimes two key problems. After reviewing the major point of the previous lesson and introducing the topic for today's lesson, the teacher presents the first problem. The problem is usually one that students do not know how to solve immediately but for which they have learned some crucial concepts or procedures in their previous lessons. Students are asked to work on the problem for a specified number of minutes and then to share their solutions. The teacher reviews and highlights one or two aspects of the students' solution methods or presents another solution method. Sometimes this cycle is repeated with another problem; other times, students practice the highlighted method or the teacher elaborates it further. Before the lesson ends, the teacher summarizes the major point for the day. Homework is rarely assigned.

Of course, not all teachers in each country teach in these ways, and not all lessons follow these scripts. But what is striking, when viewing the videotapes across the two countries, is how many of the lessons appear consistent with these scripts.

How do teachers view reform? It is interesting to note that in some respects Japanese lessons appear consistent with reform recommendations proposed by such documents as the Professional Standards for Teaching Mathematics of the National Council of Teachers of Mathematics (NCTM). Japanese lessons include high-level mathematics, a clear focus on thinking and problem solving, and an emphasis on students' deriving alternative solution methods and explaining their thinking. In other respects, though, Japanese lessons do not follow such reform guidelines. They include more lecturing and demonstration than even the more traditional U.S. lessons, and we never observed calculators being used in a Japanese classroom.

Regardless of whether Japanese classrooms share features of "reform" classrooms or not, it is quite clear that the typical U.S. classrooms do not. This is especially interesting given the fact that the U.S. teachers, when asked if they were aware of current ideas about the best ways to teach mathematics, responded overwhelmingly in the affirmative. The vast majority reported having read the NCTM standards. Seventy percent of the teachers even claimed to be implementing such ideas in the very lesson that we videotaped. It may be that teachers have changed some features of their instruction and have adopted such reforms as using real-world problems, manipulatives, or cooperative learning. But our data suggest that these changes have not affected the deeper cultural scripts from which teachers work.10 U.S. teachers are still emphasizing the acquisition and application of skills.

Beware of Simple Solutions

Given the high mathematics achievement of Japanese students,11 it is tempting to conclude that U.S. teachers should teach more like their Japanese counterparts. Although there are probably many useful ideas for U.S. classrooms in the Japanese videos, we are pessimistic that such ideas can simply be imported. Indeed, if teaching could be changed by just disseminating ideas, the record of reform in the U.S. would be more successful than it is. The data on how teachers view reform, presented above, are quite sobering in this regard.

Besides the ineffectiveness of just disseminating prescriptions, systems of teaching are not easily transported from one culture into another. Teaching, as a cultural activity, fits within a variety of social, economic, and political forces in our society. The effects of teaching are determined, in part, by all of these forces. Thus if one imports a system of teaching into a different culture, one cannot expect that system to produce the same results. The Japanese system of teaching is enmeshed within Japanese culture -- the social and behavioral norms; the expectations and involvement of parents; the national curriculum; outside educational activities such as juku (so-called cram schools); values of education held by students, parents, and the public; and so on. All these factors no doubt play important roles in supporting the kind of teaching we see on the Japanese videotapes.

An additional problem with simple solutions for improving teaching is that they often focus on individual features of teaching, such as using concrete materials, asking higher-order questions, or forming cooperative groups. But teaching is not just a collection of individual features. It is a system composed of tightly connected elements. And the system is rooted in deep-seated beliefs about the nature of the subject, the way students learn, and the role of the teacher. Attempts to change individual features are likely to have little effect on the overall system. The changes often get swallowed up or reshaped.

If we cannot improve teaching by importing another system or by manipulating individual features, what can we do? A recently popular approach is to create content and performance standards and then hold teachers accountable for achieving them. Although we firmly believe that such standards are necessary, a focus on standards and accountability that ignores the processes of teaching and learning in classrooms will not provide the direction that teachers need in their quest to improve.

Another common American approach is to ask experts to meet and discuss the problem and issue written documents to guide a reform. Reforms are needed, presumably, because past policies have failed. The experts decide that we need to break with current practice and try something new. Current documents contain recommendations for such things as how schools should be structured, how market forces should drive improvements, and how technology should change the classroom. This approach, too, is problematic because it assumes that these changes will automatically improve the quality of teaching.

Improving Classroom Teaching

What we need to improve teaching over time is an approach that recognizes that teaching can be studied and improved but at the same time acknowledges the cultural complexity and embeddedness of teaching. How can we break out of our conventional approaches and imagine more productive alternatives? Comparative studies are especially helpful here, and this is where we can learn something from the Japanese.

The approach to improving teaching used in Japan is not based on distributing written reports, or on reforming features of instruction, or on assuming that teaching will change when surrounding elements change. It is based on the direct study of teaching, with the goal of steady improvement in the mathematics learning of students.12

The process of professional teacher development in Japan begins with clearly stated goals for student learning. Japanese mathematics teachers are very familiar with the widely shared goals for student learning at each grade level. The documents that present these goals are similar to the content standards that have received so much attention in the U.S. in recent years. To the extent that American teachers share these goals and understand their meaning and intent, these standards can set the stage for improving teaching. Unfortunately, the reading of the standards documents is often the end of the process in the U.S.; in Japan, becoming familiar with the learning goals is only the beginning.

During their careers, Japanese teachers engage in a relentless, continuous process of improving their lessons to improve students' opportunities to achieve the learning goals. A key part of this process is their participation in "lesson study groups." Small groups of teachers meet regularly, once a week for about an hour, to plan, implement, evaluate, and revise lessons collaboratively. Many groups focus on only a few lessons over the course of the year with the aim of perfecting these.13

A group of fourth-grade teachers, for example, might be dissatisfied with its current lessons on adding fractions with unlike denominators. So this study group sets the goal of replacing these lessons. The group designs several lessons, one group member tries them out while the others observe and evaluate what is effective and what is not, and they revise the lessons. Maybe they change the wording of the opening problem, or maybe they change the kinds of follow-up questions they ask, or maybe they learn more about what methods students are likely to invent and then build these methods into the whole-class discussion. Then they try out the lessons again, perhaps with other teachers observing. This process may go on for several years. When the replacement lessons are ready, they are shared with other teachers, in other schools. Through the lesson study groups, teachers improve their own pedagogy and they improve the curriculum. More than that, they improve the collective practice of teaching as they share their work with others.

The belief that drives these lesson study groups is that students' opportunities to learn will improve with better lessons and that better lessons come through collaborative planning and testing. Japanese teachers assume that this task is so big that every teacher must be involved; the wisdom and experience of all teachers are needed to make progress. Further, they assume that improvement will come through a steady, gradual, cumulative process. As they learn from their experiences and pool their information, they will become more highly skilled teachers who have access to increasingly more effective lessons. By focusing on lessons, the Japanese teacher development system formulates and assesses new ideas in the same context in which these ideas will be applied. In this way, the Japanese lesson study group respects the cultural complexity of teaching, focusing on contexts in which all relevant parts of the system of instruction are naturally incorporated.

The True Profession of Teaching

The Japanese approach to teacher development stands in stark contrast to the American approach. Our biggest long-term problem is not how we teach now but that we have no way of getting better. We have no mechanism built into the teaching profession that allows us to improve gradually over time. We have reports of individual teachers who, through heroic efforts of their own, become unusually effective. But these are individuals, not large numbers of teachers, and, sadder still, we have no way of learning from their experiences. Indeed, we have no way of harvesting the best ideas of the thousands of teachers who work, by themselves, to improve their own teaching.

There are many reasons for the absence of a systemic approach to teacher development in the U.S. For example, Americans hold the notion that good teaching comes through artful and spontaneous interactions with students during lessons. This kind of on-the-fly decision making is made possible by the innate intuitions of "natural" teachers. Such views minimize the importance of planning increasingly effective lessons and lend credence to the folk belief that good teachers are born, not made. If we really believe this, it is no wonder that teacher development is not a high priority. Unfortunately, it is not just one belief, but an entire cluster of beliefs, some of them contradictory, that dampen our commitment to improving teaching. Beliefs about teacher autonomy; about the intractable complexity of teaching, on the one hand, and its common simplicity, on the other; about the unlikelihood that it will ever change, on the one hand, and the persistent optimism of reformers, on the other - all these tenets work against efforts to institute mechanisms for continuous, long-term improvement.

We are not arguing for simply importing the Japanese method of teacher development. Just as the Japanese method of teaching mathematics is embedded in a particular culture, so is the Japanese system of teacher development. However, in both cases, we can study these alternative systems to gain new insights into our own systems, and we can use these insights to challenge the status quo.

We believe that our failure to take teacher development seriously is closely tied to the issue of professionalism. For years, educators have called attention to the relatively low status of teaching and have bemoaned the lack of respect bestowed on teaching by the media and the public. Much rhetoric has been devoted to this issue, as if demanding higher status or labeling teaching a profession would solve the problem. A true profession of teaching will emerge as teachers find ways and are given the opportunities to improve teaching. By improving teaching, we mean a relentless process in which teachers do not just improve their own skills but also contribute to the improvement of Teaching with a capital T. Only when teachers are allowed to see themselves as members of a group, collectively and directly improving their professional practice by improving pedagogy and curricula and by improving students' opportunities to learn, will we be on the road to developing a true profession of teaching. The TIMSS videotape study points us beyond the data, not to a critique of how we currently teach but to a recognition of the need to implement a mechanism whereby we can, over time, improve our teaching.

2. A number of researchers have pointed out that teachers teach much in the way they were taught. See, for example, Daniel C. Lortie, Schoolteacher: A Sociological Study (Chicago: University of Chicago Press, 1975); and Sharon F. Nemser, "Learning to Teach," in Lee Shulman and Gary Sykes, eds., Handbook of Teaching and Policy (New York: Longman, 1983), pp. 150-70.

3. A complete description of sampling procedures can be found in James W. Stigler et al., The TIMSS Videotape Classroom Study: Methods and Findings from an Exploratory Research Project on Eighth-Grade Mathematics Instruction in Germany, Japan, and the United States (Washington, D.C.: National Center for Education Statistics, 1997).

4. For a full description of videotaping considerations and procedures, see Stigler et al., op. cit.

5. Professional Standards for Teaching Mathematics (Reston, Va.: National Council of Teachers of Mathematics, 1991).

6. Richard E. Nisbett and Lee Ross, Human Inference: Strategies and Shortcomings of Social Judgment (Englewood Cliffs, N.J.: Prentice-Hall, 1980).

7. For a complete report of the 41-country curriculum analysis, see William H. Schmidt et al., Many Visions, Many Aims: A Cross-National Investigation of Curricular Intentions in School Mathematics (Boston: Kluwer, 1997).

8. The Math Group was led by Alfred Manaster of the University of California, San Diego. Other members of the group were Phillip Emig, Wallace Etterbeek, and Barbara Wells.

9. A videotape with examples from German, Japanese, and U.S. lessons, together with an accompanying study guide, can be obtained by phoning the National Center for Education Statistics at 202/219-1333 or by sending e-mail to timss@ed.gov.

10. Other studies have also shown that reform recommendations are often implemented in superficial ways. See, for example, the case studies of California teachers conducted by researchers from Michigan State University and reported in a special issue of Educational Evaluation and Policy Analysis (Fall 1990).

11. TIMSS achievement results for eighth grade are published in Lois Peak, Pursuing Excellence: A Study of U.S. Eighth-Grade Mathematics and Science Teaching, Learning, Curriculum, and Achievement in International Context (Washington, D.C.: Office of Educational Research and Improvement, U.S. Department of Education, 1996).

12. Our description of the Japanese process of improving teaching comes from our conversations with Japanese educators and a number of written sources, including Nobuo K. Shimahara and Akira Sakai, Learning to Teach in Two Cultures: Japan and the United States (New York: Garland, 1995); and two special issues of the Peabody Journal of Education devoted to Japanese teacher education (Spring and Summer 1993).

13. For more information on lesson study in Japan, see Catherine Lewis and Ineko Tsuchida, "Planned Educational Change in Japan: The Shift to Student-Centered Elementary Science," Journal of Educational Policy, in press.